5 класс. Математика. Виленкин. Учебник. Ответы к стр. 47
Натуральные числа
Сложение и вычитание натуральных чисел
Вычитание
Ответы к стр. 47
274. Составьте условие задачи, решением которой служит выражение:
а) 26 + 15 - 7; 6) 53 - 4 - 11 + 5.
а) В автобусе ехали 26 пассажиров. На остановке вышли 7 пассажиров и зашли 15 пассажиров. Сколько пассажиров стало в автобусе?
б) В библиотеке было 53 журнала. Утром взяли 4 журнала, после обеда взяли ещё 11 журналов, а вечером вернули 5 журналов. Сколько журналов стало в библиотеке?
275. На координатном луче отмечены точки О(0), А(12), В(7). На сколько единичных отрезков отрезок ОА длиннее отрезка ОВ?
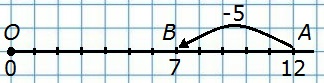
ОА - ОВ = 12 - 7 = 5 (ед. отр.)
276. Проверьте, помните ли вы, что означают слова «отрезок», «прямая», «луч», «дополнительные лучи». Объясните значения этих слов.
Отрезок - это часть прямой, ограниченная двумя точками: первая точка - начало отрезка, вторая точка - конец отрезка.
Прямая - это линия, которая не искривляется и не имеет начала и конца: прямую можно бесконечно продолжать в обе стороны.
Луч - это часть прямой, которая имеет начало и не имеет конца: луч можно бесконечно продолжать только в одну сторону.
Дополнительные лучи - это лучи, которые получаются когда точка делит прямую на два луча.
277. Установите правило нахождения числа, стоящего в средней клетке первой строки, и по этому правилу вставьте в пустую клетку пропущенное число.
а) [15] [41] [26]
[19] [31] [12]
Число в средней клетке равно сумме чисел в крайних клетках.
б) [19] [18] [37]
[17] [29] [46]
Число в средней клетке равно разности крайнего правого и крайнего левого чисел.
в) [51] [3] [17]
[57] [3] [19]
Число в средней клетке равно частному при делении крайнего левого числа на крайнее правое число.
278. Как найти периметр прямоугольника; квадрата? Предложите разные способы. Какие из этих способов лучше?
Периметр любой геометрической фигуры (прямоугольник, квадрат) - это сумма длин всех его сторон.
Периметр прямоугольника (противоположные стороны равны):
- сумма длин всех его сторон: α + b + α + b;
- сумма удвоенных длин его противополжных сторон: 2 • α + 2 • b;
- удвоенная сумма его соседних сторон: 2 • (α + b) - наилучший способ.
Периметр квадрата (все стороны равны):
- сумма длин всех его сторон: α + α + α + α;
- учетверённая сторона: 4 • α - наилучший способ.
279. На железнодорожной станции стояли 3 товарных состава. В первом составе было 30 вагонов, во втором - на 5 вагонов больше, чем в первом. Сколько всего вагонов было в этих трёх составах, если в первом из них было на 10 вагонов меньше, чем в третьем?
1) 30 + 5 = 35 (в.) - во втором составе
2) 30 + 10 = 40 (в.) - в третьем составе
3) 30 + 35 + 40 = 105 (в.) - всего
О т в е т: в трёх составах 105 вагонов.
280. Выполните сложение:
а) 28 999 000 145 + 39 001 789 259;
б) 1 234 567 890 + 8 765 432 108.
+ 28 999 000 145 + 1 234 567 890
39 001 789 259 8 765 432 108
68 000 789 404 9 999 999 998
281. Что больше:
а) 7508 + 8534 или 17 000;
б) 24 645 + 39 815 или 35 678 + 40 961?
а) + 7508
8534
16 042
16 042 < 17 000
б) + 24 645 + 35 678
39 815 40 961
64 460 76 639
64 460 < 76 639
282. Сравните числа, в которых некоторые цифры заменены звёздочками:
а) 7∗∗∗∗ и 69∗∗∗; в) ∗∗∗∗∗ и ∗∗∗;
б) 85∗∗∗ и 13∗∗∗; г) ∗8∗∗ и 99∗∗.
а) 7∗∗∗∗ > 69∗∗∗ - оба числа пятизначные, но у первого числа цифра в разряде десятков тысяч (7) больше аналогичной цифры (6) у второго числа;
б) 85∗∗∗ > 13∗∗∗ - оба числа пятизначные, но у первого числа цифра в разряде десятков тысяч (8) больше аналогичной цифры (1) у второго числа;
в) ∗∗∗∗∗ > ∗∗∗ - первое число пятизначное, а второе - трёхзначное, следовательно, первое число больше;
г) ∗8∗∗ < 99∗∗ - если первая цифра (разряд тысяч) первого числа будет 9, то сравнение идёт по второй цифре (разряд сотен), а 8 < 9.
283. Сколько двузначных чисел можно составить из цифр 0, 2, 4, 6, если цифры в записи числа не повторяются? Запишите все эти числа.
Число не может начинаться с нуля, поэтому первой цифрой может быть 2 или 4 или 6.
Если первая цифра 2, то второй цифрой может быть 0 или 4 или 6: 20, 24, 26.
Если первая цифра 4, то второй цифрой может быть 0 или 2 или 6: 40, 42, 46.
Если первая цифра 6, то второй цифрой может быть 0 или 2 или 4: 60, 62, 64.
Всего получается 9 чисел.
284. Решите задачу:
1) Периметр треугольника 28 см, а периметр прямоугольника в 4 раза больше. На сколько сантиметров периметр треугольника меньше периметра прямоугольника?
2) Периметр треугольника 36 см, а периметр прямоугольника в 3 раза меньше. На сколько сантиметров периметр треугольника больше периметра прямоугольника?
1) 1) 28 • 4 = 112 (см) - периметр прямоугольника
2) 112 - 28 = 84 (см) - меньше периметр треугольника
О т в е т: периметр треугольника меньше на 84 см.
2) 1) 36 : 3 = 12 (см) - периметр прямоугольника
2) 36 - 12 = 24 (см) - больше периметр треугольника
О т в е т: периметр треугольника больше на 24 см.
285. Выполните действия:
1) 44 - 24 • 18 : 36; 3) (83 • 250 - 14 918) : 54;
2) 1863 : 23 • 11 - 2; 4) (3885 : 37 + 245) • 78.
1) 44 - 24 • 18 : 36 = 32;
× 24 _ 432|36 _ 44
18 36 |12 12
+ 192 _ 72 32
24 72
432 0
2) 1863 : 23 • 11 - 2 = 889;
_ 1863|23 × 81 _ 891
184 |81 11 2
_ 23 + 81 889
23 81
0 891
3) (83 • 250 - 14 918) : 54 = 108;
× 83 _ 20 750 _ 5832|54
250 14 918 54 |108
+ 415 5832 _432
166 432
20 750 0
4) (3885 : 37 + 245) • 78 = 27 300.
_ 3885|37 + 105 × 350
37 |105 245 78
_ 185 350 + 280
185 245
0 27 300
| ← Предыдущая | Следующая → |
Ответы по математике. 5 класс. Учебник. Виленкин Н. Я., Жохов В. И., Чесноков А. С., Шварцбурд С. И
