9 класс. Геометрия. Атанасян Л.С. Учебник. Ответы к стр. 246 Дополнительные задачи к главе X. Метод координат
ГДЗ. Ответы по геометрии. 9 класс. Учебник. Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Позняк Э.Г., Юдина И.И.

Глава Х Метод координат
Дополнительные задачи к главе X. Метод координат
№992 Докажите, что треугольник АВС, вершины которого имеют координаты А (4; 8), В (12; 11), С (7; 0), является равнобедренным, но не равносторонним.
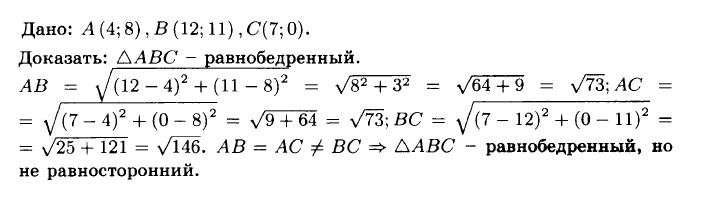
№993 Докажите, что углы А и С треугольника АВС равны, если А (—5; 6), В (3; —9) и С (—12; —17).
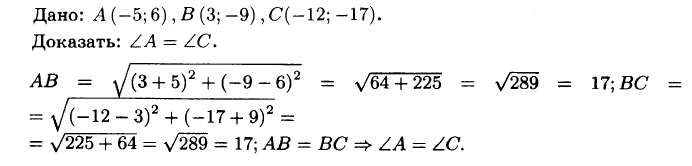
№994 Докажите, что точка D равноудалена от точек А, В и С, если:
а) D (1; 1), А (5; 4), В (4; —3), С (—2; 5);
б) D (1; 0), А (7; —8), В (—5; 8), С (9; 6).
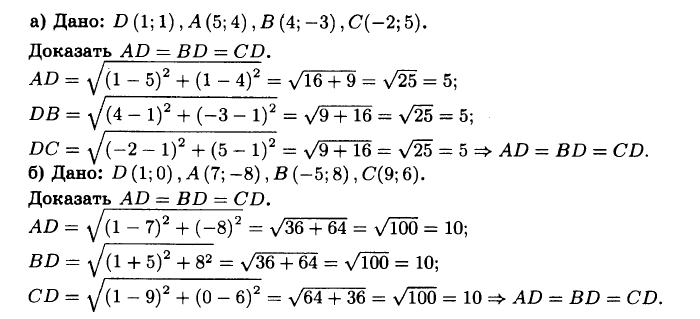
№995 На оси абсцисс найдите точку, равноудалённую от точек М, (-2; 4) и М2 (6; 8).
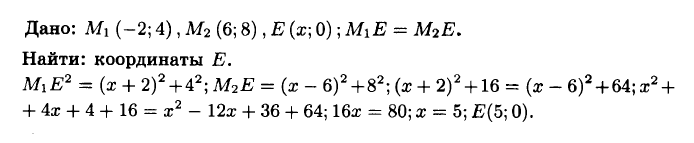
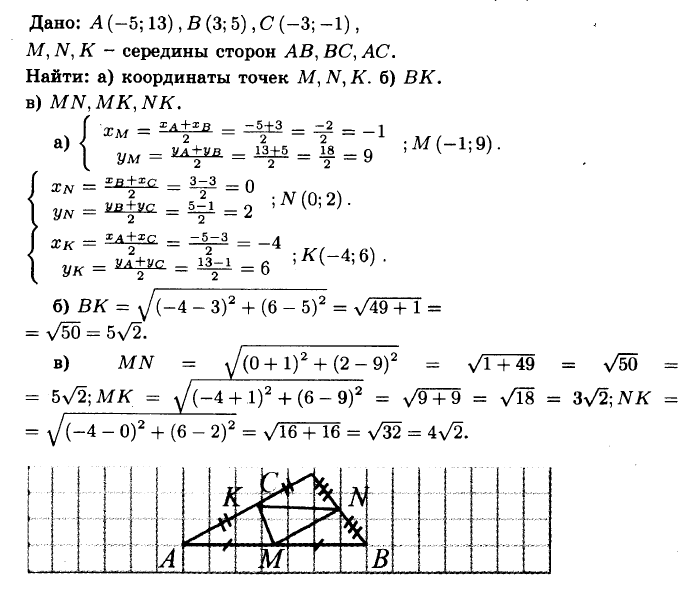
№996 Вершины треугольника АВС имеют координаты А (—5; 13), В (3; 5), С (—3; —1). Найдите:
а) координаты середин сторон треугольника;
б) медиану, проведённую к стороне АС;
в) средние линии треугольника.
№997 Докажите, что четырёхугольник ABCD, вершины которого имеют координаты А (3; 2), В (0; 5), С (—3; 2), D (0; —1), является квадратом.

№998 Докажите, что четырёхугольник ABCD, вершины которого имеют координаты А (—2;—3), 13 (1; 4), С (8; 7), D (5; 0), является ромбом. Найдите его площадь.
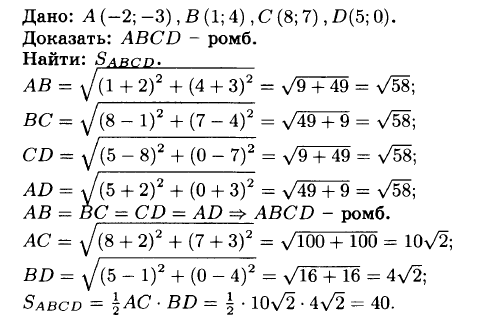
№999 Найдите координаты четвёртой вершины параллелограмма по заданным координатам трёх его вершин: (—4; 4), (—5; 1) и (—1; 5). Сколько решений имеет задача?

№1000 Выясните, какие из данных уравнений являются уравнениями окружности. Найдите координаты центра и радиус каждой окружности:
а) (х — 1)2 + (y + 2)2 = 25;
б) х2 + (у + 7)2 = 1;
в) х2 + у2 + 8х — 4у + 40 = 0;
г) х2 + у2 — 2х + 4у - 20 = 0;
д) х2 + у2 — 4х — 2у + 1 =0.

№1001 Напишите уравнение окружности, проходящей через точки А (3; 0) и В (—1; 2), если центр её лежит на прямой у = х + 2.

№1002 Напишите уравнение окружности, проходящей через три данные точки:
а) А (1; —4), В (4; 5), С (3; —2);
б) А (3; —7), В (8; —2), С (6; 2).

№1003 Вершины треугольника АВС имеют координаты А (—7; 5), В (3; —1), С (5; 3). Составьте уравнения:
а) серединных перпендикуляров к сторонам треугольника;
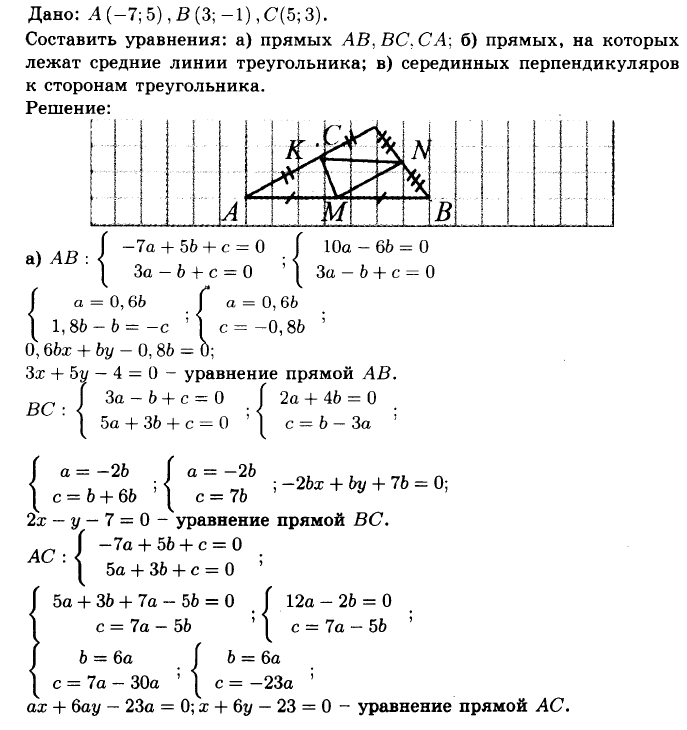
б) прямых АВ, ВС и СА;

в) прямых, на которых лежат средние линии треугольника.

№1004 Докажите, что прямые, заданные уравнениями 3х — 1,5y + 1 = 0 и 2х — у — 3 = 0, параллельны.
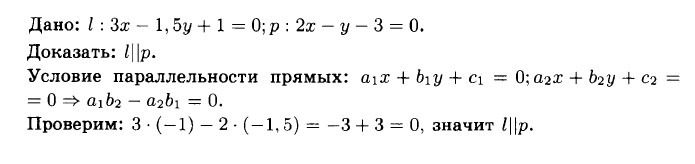
← Предыдущая Следующая →
