5 класс. Математика. Виленкин. Учебник. Ответы к стр. 63
Натуральные числа
Сложение и вычитание натуральных чисел
Уравнение
Ответы к стр. 63
382. Вычислите устно:
а) 15 • 6 в) 100 - 19 д) 60 - 11
90 : 18 81 : 3 49 : 7
5 • 19 27 + 23 7 • 15
95 + 6 50 • 4 105 - 25
101 200 80
б) 88 - 19 г) 80 - 16
69 : 23 64 : 8
3 • 15 8 • 11
45 + 55 88 + 22
100 110
383. На координатном луче даны точки А(18), В(7), С(31), D(27), Е(23), О(0). Какие из этих точек:
а) левее точки E и на сколько единичных отрезков;
б) правее точки А и на сколько единичных отрезков;
в) расположены между точками В и D?

а) точка А на 23 - 18 = 5 единичных отрезков, точка В на 23 - 7 = 16 единичных отрезков, точка О на 23 - 0 = 23 единичных отрезка;
б) точка Е на 23 - 18 = 5 единичных отрезка, точка D на 27 - 18 = 9 единичных отрезка, точка С на 31 - 18 = 13 единичных отрезка;
в) точка А(18) и точка Е(23).
384. Что больше и во сколько раз:
а) два часа или сорок минут;
б) десять центнеров или две тонны;
в) шесть сантиметров или двадцать миллиметров?
а) 2 ч = 120 мин, 120 : 40 = 3 - в 3 раза больше 2 часа;
б) 2 т = 20 ц, 20 : 10 = 2 - в 2 раза больше 2 тонны,
в) 20 мм = 2 см, 6 : 2 = 3 - в 3 раза больше 6 сантиметров.
385. В бидоне 24 л молока. Для приготовления завтраков израсходовали четвёртую часть молока, а для приготовления обедов - половину оставшегося молока. Сколько литров молока осталось в бидоне?
1) 24 : 4 • 1 = 6 (л) - ушло на завтраки
2) 24 - 6 = 18 (л) - осталось после завтраков
3) 18 : 2 = 9 (л) - ушло на обеды
4) 18 - 9 = 9 (л) - осталось в бидоне
О т в е т: в бидоне осталось 9 л молока.
386. Найдите пропущенное число:
а) [13] [60] [17]
[16] [60] [14] - число посередине равно удвоенной сумме крайних чисел;
б) [26] [20] [14]
[19] [25] [31] - число посередине равно частному суммы крайних чисел и числа 2.
387. Вместо некоторых цифр поставлены звёздочки. Можно ли сравнить числа:
а) 32∗∗ и 31∗∗; б) ∗1∗∗ и 8∗∗; в) ∗∗∗∗ и ∗∗∗; г) ∗5∗ и 1∗∗?
а) оба числа четырёхзначные, первые цифры у них равны, значит, сравнивают вторые цифры - первое число больше;
б) первое число четырёхзначное, а второе - трёхзначное, значит, первое число будет больше в любом случае;
в) первое число четырёхзначное, а второе - трёхзначное, значит, первое число будет больше в любом случае;
г) оба числа трёхзначные и нельзя сравнить их первые и вторые цифры, значит, сравнить эти числа нельзя.
388. Из села Аникеево в село Большово ведут четыре дороги, а из села Большово в село Виноградово - три дороги. Сколькими способами можно добраться из Аникеева в Виноградово через село Большово?
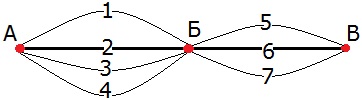
Р е ш е н и е.
Если из А в Б добираться по 1-й дороге, то продолжить путь есть три способа:
5—• В
Б/
А •—1—•—6—• В
\
7—• В
Точно так же рассуждая, получаем по три способа продолжить путь, начав добираться и по 2-й, и по 3-й, и по 4-й дороге. Значит, всего получается 4 • 3 = 12 способов добраться из Аникеева в Виноградово.
| ← Предыдущая | Следующая → |
Ответы по математике. 5 класс. Учебник. Виленкин Н. Я., Жохов В. И., Чесноков А. С., Шварцбурд С. И
