8 класс. Алгебра. Никольский. Учебник. Ответы к стр. 13

8 класс. Алгебра. Никольский. Учебник. Ответы к стр. 13

Простейшие функции. Квадратные корни
Функции и графики
Координатная ось. Модуль числа

Ответы к стр. 13

20. Укажите на координатной оси числа:
а) -5 и 0,31; б) 15,57 и 5,176;
в) -π и π²; г) -5 ¹/₃ и 4,01.

兀 ≈ 3,14, 兀² ≈ 9,86

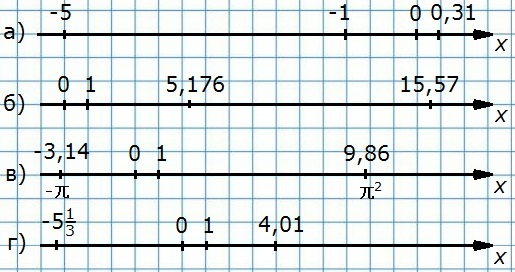
21. Укажите хотя бы три числа, находящиеся на координатной оси между числами:
а) 3,11 и 3,12; б) 2,082 и 2,081;
в) ¹/₈ и ¹/₉;      г) 3,5 и 3 ⁴/₉.

а) 3,11 < 3,111 < 3,112 < 3,113 < 3,12;
б) 2,082 > 2,0819 > 2,0818 > 2,0817 > 2,081;
в) ¹/₈ = 0,125, ¹/₉ = 0,(1),
0,125 > 0,124 > 0,123 > 0,122 > 0,(1);
г) 3 ⁴/₉ = 3,(4),
3,5 > 3,49 > 3,48 > 3,47 > 3,(4).

22. а) Каждой ли точке координатной оси поставлено в соответствие число?
б) Каждому ли числу поставлена в соответствие точка координатной оси?

а) Каждой точке на координатной оси ставится в соответствие действительное число.
б) Каждому числу  ставится в соответствие точка на координатной прямой. Между точками на координатной оси и действительными числами установлено взаимно-однозначное соответствие.

23. Решите уравнение:
а) |x| = 5;                       б) |2х - 3| = 7;
в) ||x| - 2| = 4;              г) ||х| - 4| = 2;
д) ||2x - 5| - 1| = 7;       е) ||2х - 1| - 5| = 7;
ж) ||2x - 7| - 5| = 1;      з) |х - 1| = |2х - 4|;
и) |3х + 2| = |5х + 6|; к) |3х - 1| = |х - 5|.

а) |x| = 5,
х₁ = 5, х₂ = -5;

б) |2х - 3| = 7,
2х - 3 = 7   2х - 3 = -7,
2х = 10      2х = -4,
х₁ = 5        х₂ = -2;

в) ||x| - 2| = 4,
|x| - 2 = 4   |x| - 2 = -4,
|x| = 6        |x| = -2 - не имеет решений,
х₁ = -6, х₂ = 6;

г) ||х| - 4| = 2,
|х| - 4 = 2   |х| - 4 = -2,
|х| = 6        |х| = 2,
х₁ = 6, х₂ = -6, х₃ = 2, х₄ = -2;

д) ||2x - 5| - 1| = 7,
|2x - 5| - 1 = 7   |2x - 5| - 1 = -7 - не имеет решений,
|2x - 5| = 8,
2x - 5 = 8   2x - 5 = -8,
2х = 13      2х = -3,
х₁ = 6,5     х₂ = -1,5;

е) ||2х - 1| - 5| = 7,
|2х - 1| - 5 = 7   |2х - 1| - 5 = -7 - не имеет решений,
|2х - 1| = 12,
2х - 1 = 12   2х - 1 = -12,
2х = 13        2х = -11,
х₁ = 6,5       х₂ = -5,5;

ж) ||2x - 7| - 5| = 1,
|2x - 7| - 5 = 1   |2x - 7| - 5 = -1,
|2x - 7| = 6   |2x - 7| = 4,
2x - 7 = 6   2x - 7 = -6   2x - 7 = 4   2x - 7| = -4,
2х = 13      2х = 1          2х = 11      2х = 3,
х₁ = 6,5     х₂ = 0,5        х₃ = 5,5     х₄ = 1,5;

з) |х - 1| = |2х - 4|,
х - 1 = 2х - 4   х - 1 = -(2х - 4),
х₁ = 3             х₂ = 1 ²/₃;

и) |3х + 2| = |5х + 6|,
3х + 2 = 5х + 6   3х + 2 = -(5х + 6),
х₁ = -2                х₂ = -1;

к) |3х - 1| = |х - 5|,
3х - 1 = х - 5   3х - 1 = -(х - 5),
х₁ = -2            х₂ = 1 ¹/₂.

24. Исследуем. Найдите значение α, при котором уравнение:
а) |2х - 4| = |х - α|; б) |3х - 2| = |х - α|
имеет единственный корень.

а) |2х - 4| = |х - α|,
2х - 4 = х - α   2х - 4 = -(х - α),
х₁ = 4 - α        х₂ = (α + 4) : 3,
Уравнение имеет единственный корень, если х₁ = х₂:
4 - α = (α + 4) : 3,
α = 2;

б) |3х - 2| = |х - α|,
3х - 2 = х - α   3х - 2 = -(х - α)
х₁ = (2 - α) : 2   х₂ = (α + 2) : 4,
Уравнение имеет единственный корень, если х₁ = х₂:
(2 - α) : 2 = (α + 2) : 4,
α = ²/₃.

Доказываем (25-28)

25. Докажите свойства 1—6 модуля числа.

Свойство 1: |-α| = |α|.
Доказательство. |-α| = α, |α| = α ⇒ |-α| = |α|.

Свойство 2: α ≤ |α|.
Доказательство. Если α > 0, то |α| = α, если α < 0, то |α| > α ⇒ |α| ≥ α.

Свойство 3: |α • b| = |α| • |b|.
а) Если α > 0, b > 0, то |α| = α и |b| = b (|α| • |b| = αb), а |α • b| = αb ⇒ |α • b| = |α| • |b|.
б) Если α < 0, b < 0, то |-α| = α и |-b| = b (|-α| • |-b| = αb), а |α • b| = |(-α) • (-b)| = αb ⇒ |α • b| = |α| • |b|.
в) Если α < 0, b > 0, то |-α| = α и |b| = b (|-α| • |b| = αb), а |α • b| = |(-α) • b| = |-αb| = αb ⇒ |α • b| = |α| • |b|.
г) Если α > 0, b < 0, то |α| = α и |-b| = b (|α| • |-b| = αb), а |α • b| = |α • (-b)| = |-αb| = αb ⇒ |α • b| = |α| • |b|.

Свойство 4: |^α/_b| = ^|α|/_|b|.
Доказательство. а) Если α > 0, b > 0, то |α| = α и |b| = b (^|α|/_|b| = ^α/_b), а |^α/_b| = ^α/_b ⇒ |^α/_b| = ^|α|/_|b|.
б) Если α < 0, b < 0, то |-α| = α и |-b| = b (^|-α|/_|-b| = ^α/_b), а |^α/_b| = |^(-α)/_(-b)| = ^α/_b ⇒ |^α/_b| = ^|α|/_|b|.
в) Если α < 0, b > 0, то |-α| = α и |b| = b (^|-α|/_|b| = ^α/_b), а |^α/_b| = |^(-α)/_b| = |- ^α/_b| = ^α/_b ⇒ |^α/_b| = ^|α|/_|b|.
г) Если α > 0, b < 0, то |α| = α и |-b| = b (^|α|/_|-b| = ^α/_b), а |^α/_b| = |^α/_(-b)| = |- ^α/_b| = ^α/_b ⇒ |^α/_b| = ^|α|/_|b|.

Свойство 5: |α + b| ≤ |α| + |b|.
Доказательство. а) Если α > 0, b > 0, то |α| = α и |b| = b (|α| + |b| = α + b), а |α + b| = α + b ⇒ |α + b| = |α| + |b|.
б) Если α < 0, b < 0, то |-α| = α и |-b| = b (|-α| + |-b| = α + b), а |α + b| = |-α - b| = |-(α + b)| = α + b ⇒ |α + b| = |α| + |b|.
в) Если α < 0, b > 0, то |-α| = α и |b| = b (|-α| + |b| = α + b), а |α + b| = |-α + b| = |-(b - α)| = |b - α| ⇒ |b - α| < |-α| + |b|, значит, |α + b| < |α| + |b|.
г) Если α > 0, b < 0, то |α| = α и |-b| = b (|α| + |-b| = α + b), а |α + (-b)| = |α - b| ⇒ |α - b| < |α| + |-b|, значит, |α + b| < |α| + |b|.

Свойство 6: |α - b| ≤ |α| + |b|.
Доказательство. а) Если α > 0, b > 0, то |α| = α и |b| = b (|α| + |b| = α + b) и |α - b| ⇒ |α - b| < |α| + |b|.
б) Если α < 0, b < 0, то |-α| = α и |-b| = b (|-α| + |-b| = α + b), а |-α - (-b)| = |-α + b| = |-(α - b)| = |α - b| ⇒ |α - b| < |α| + |b|.
в) Если α < 0, b > 0, то |-α| = α и |b| = b (|-α| + |b| = α + b), а |-α + b| = |-(b - α)| = |b - α| ⇒ |b - α| < |-α| + |b|, значит, |α + b| < |α| + |b|.
г) Если α > 0, b < 0, то |α| = α и |-b| = b (|α| + |-b| = α + b), а |α - (-b)| = |α + b| = α + b ⇒ |α - b| = |α| + |b|.

26. Докажите, что для любого числа х:
а) |15х - 16| = |16 - 15х|;         б) |х² - 7| = |7 - х²|;
в) 12х - 1 ≤ |1 - 12х|;                 г) х² - 2011 ≤ |2011 - х²|;
д) |х² - 49| = |х - 7| • |х + 7|; е) |х² - 3| = |x⁴ - 9|/|x² + 3|;
ж) |8 + 5х| ≤ |1 + 2х| + |7 + 3х|;
з) |1 + 6х| ≤ |5х - 11| + |12 + х|;
и) |2 + 4х| ≤ |6 + 7х| + |4 + 3х|;
к) |х - 23| ≤ |12х - 11| + |12 + 11х|.

а) |15х - 16| = |16 - 15х|,
|16 - 15х| = |-(15х - 16)| = |15х - 16| - свойство 1;

б) |х² - 7| = |7 - х²|,
|7 - х²| = |-(х² - 7)| = |х² - 7| - свойство 1;

в) 12х - 1 ≤ |1 - 12х|,
|1 - 12х| = |-(12х - 1)| = |12х - 1| - свойство 1,
12х - 1 ≤ |12х - 1| - свойство 2;

г) х² - 2011 ≤ |2011 - х²|,
|2011 - х²| = |-(х² - 2011)| = |х² - 2011| - свойство 1,
х² - 2011 ≤ |х² - 2011| - свойство 2;

д) |х² - 49| = |х - 7| • |х + 7|,
|х - 7| • |х + 7| = |(х - 7) • (х + 7)| - свойство 3,
|(х - 7) • (х + 7)| = |х² - 7²| = |х² - 49|;

е) |х² - 3| = |x⁴ - 9|/|x² + 3|,
|x⁴ - 9|/|x² + 3| = |(x² - 3)(x² + 3)|/|x² + 3| = |x² - 3|•|x² + 3|/|x² + 3| - свойство 3,
|x² - 3|•|x² + 3|/|x² + 3| = |x² - 3| - свойство 4;

ж) |8 + 5х| ≤ |1 + 2х| + |7 + 3х|,
|8 + 5х| ≤ |1 + 2х + 7 + 3х| - свойство 5,
|8 + 5х| ≤ |8 + 5х|;

з) |1 + 6х| ≤ |5х - 11| + |12 + х|,
|1 + 6х| ≤ |5х - 11 + 12 + х| - свойство 5,
|1 + 6х| ≤ |1 + 6х|;

и) |2 + 4х| ≤ |6 + 7х| + |4 + 3х|,
|2 + 4х| ≤ |6 + 7х + 4 + 3х| - свойство 5,
|2 + 4х| ≤ |10 + 10х|,
|10(0,2 + 0,4х)| ≤ |10(1 + х)|,
|10|•|0,2 + 0,4х| ≤ |10|•|1 + х| - свойство 3,
|0,2 + 0,4х| ≤ |1 + х|;

к) |х - 23| ≤ |12х - 11| + |12 + 11х|,
|х - 23| ≤ |12х - 11 + 12 + 11х| - свойство 6,
|х - 23| ≤ |23х + 1|,
|23(^х/₂₃ - 1)| ≤ |23(х + ¹/₂₃)|,
|23|•|^х/₂₃ - 1| ≤ |23|•|х + ¹/₂₃| - свойство 3,
|^х/₂₃ - 1| ≤ |х + ¹/₂₃|.

27. а) Докажите, что расстояние между точками А (х₁) и В (х₂) вычисляется по формуле АВ = |х₁ - х₂|.
б) Докажите, что координата точки С(х) — середины отрезка АВ, где A(x₁) и В(х₂), — вычисляется по формуле х = (x₁+x₂)/2.

а) Если х₁ > 0, х₂ > 0, х₂ > х₁, то АВ = х₂ - х₁ = |-(х₁ - х₂)| = |х₁ - х₂|.
Если х₁ < 0, х₂ < 0, х₂ > х₁, то АВ = х₂ - х₁ = |-х₂ - (-х₁)| = |х₁ - х₂|.
Если х₁ > 0, х₂ < 0, х₂ < х₁, то АВ = х₁ - х₂ = |х₁ - х₂|.

б) Если х₁ > х₂, то х₁ > х > х₂, следовательно, ВС = х - х₂, СА = х₁ - х. Так как ВС = СА, то х - х₂ = х₁ - х.
х - х₂ = х₁ - х,
х + х = х₁ + х₂,
2х = х₁ + х₂,
х = (х₁ + х₂)/2;

Если х₁ < х₂, то х₁ < х < х₂, следовательно, АС = х - х₁, СВ = х₂ - х. Так как АС = СВ, то х - х₁ = х₂ - х.
х - х₁ = х₂ - х,
х + х = х₁ + х₂,
2х = х₁ + х₂,
х = (х₁ + х₂)/2.

← Предыдущая

Следующая →

Ответы по алгебре. 8 класс. Учебник. Никольский С. М., Потапов М. К., Решетников Н. Н., Шевкин А. В.

Алгебра. 8 класс