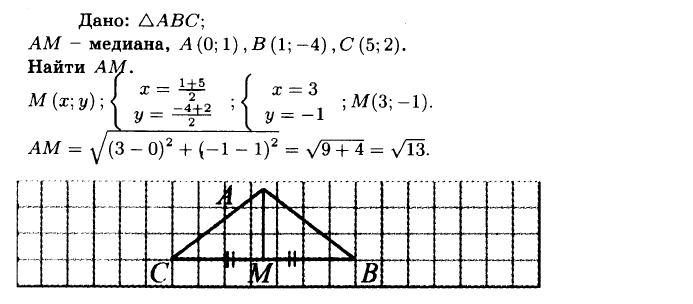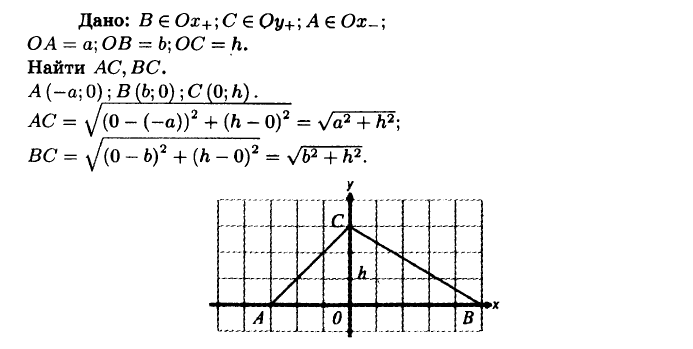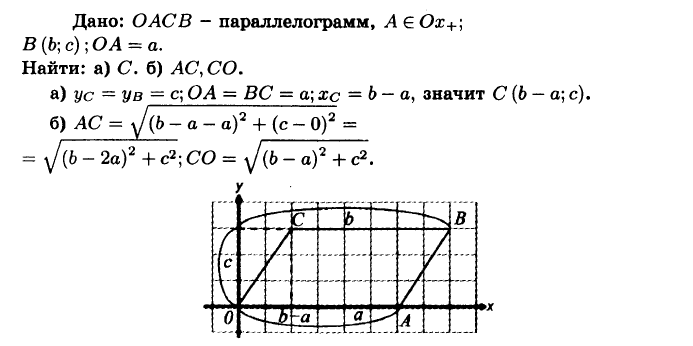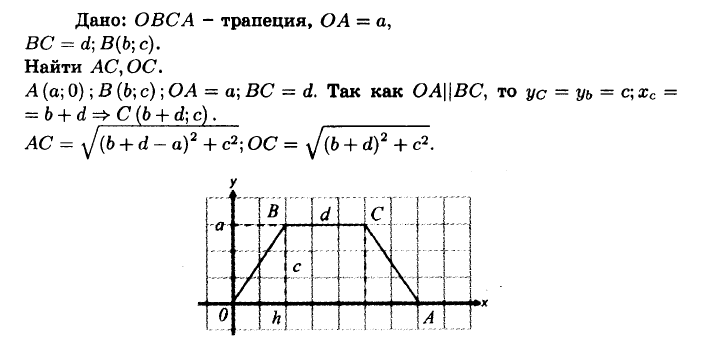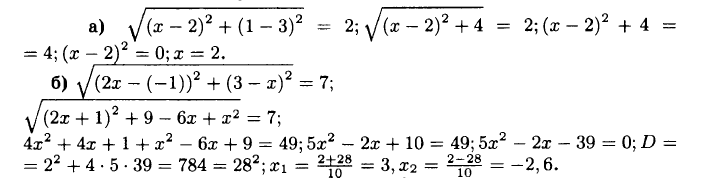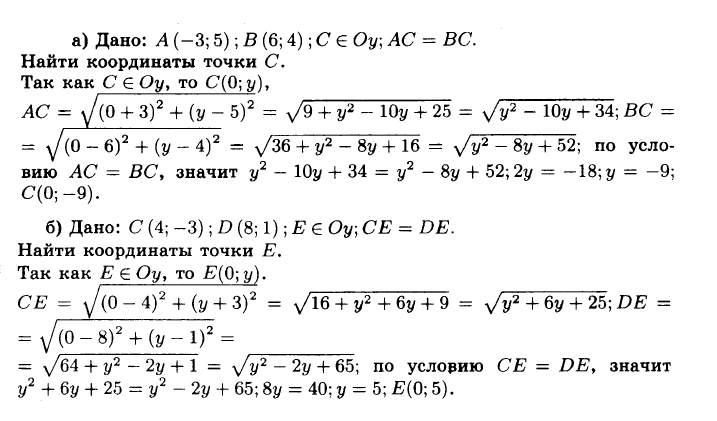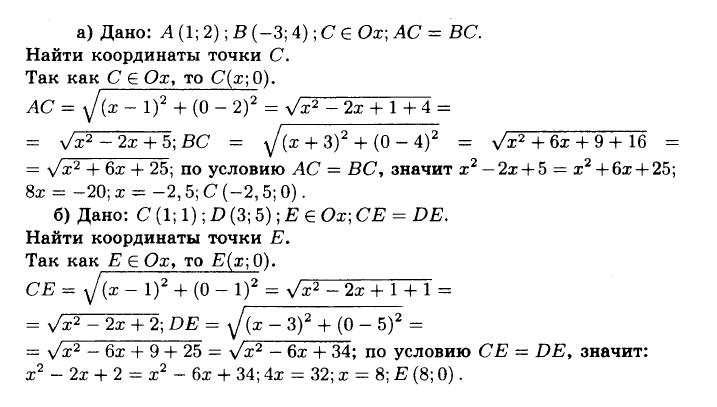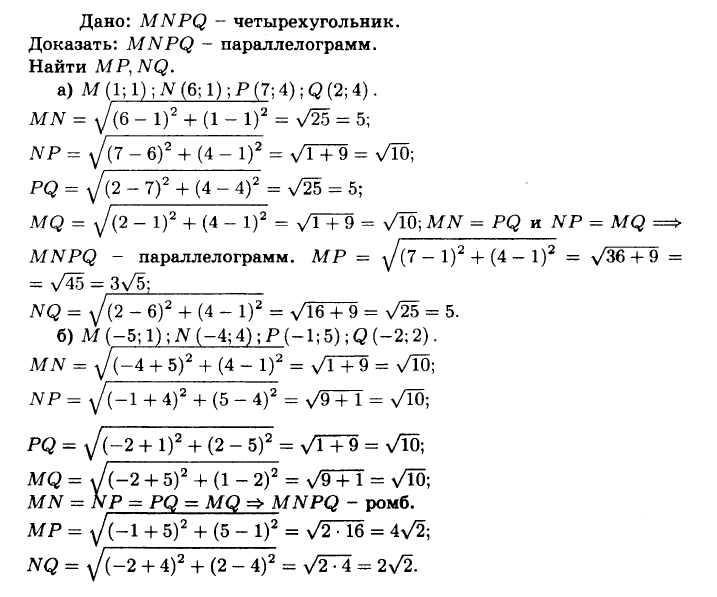Сайт для детей и любящих родителей
ГДЗ. Ответы по геометрии. 9 класс. Учебник. Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Позняк Э.Г., Юдина И.И.
Глава Х Метод координат
§2 Простейшие задачи в координатах
№957 Докажите, что если диагонали параллелограмма равны, то параллелограмм является прямоугольником.
№958 Дан прямоугольник ABCD. Докажите, что для произвольной точки М плоскости справедливо равенство AM2 + СМ2 = ВМ2 + DM2.
ГДЗ. Ответы по геометрии. 9 класс. Учебник. Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Позняк Э.Г., Юдина И.И.
Глава Х Метод координат
§2 Простейшие задачи в координатах
№953 Докажите, что сумма квадратов всех сторон параллелограмма равна сумме квадратов его диагоналей.
Решение в учебнике с. 234
№954 Медиана, проведённая к основанию равнобедренного треугольника, равна 160 см, а основание треугольника равно 80 см. Найдите две другие медианы этого треугольника.
№955 Высота треугольника, равная 10 см, делит основание на два отрезка, равные 10 см и 4 см. Найдите медиану, проведённую к меньшей из двух других сторон.
№956 Докажите, что в равнобедренной трапеции диагонали равны. Сформулируйте и докажите обратное утверждение.
ГДЗ. Ответы по геометрии. 9 класс. Учебник. Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Позняк Э.Г., Юдина И.И.
Глава Х Метод координат
§2 Простейшие задачи в координатах
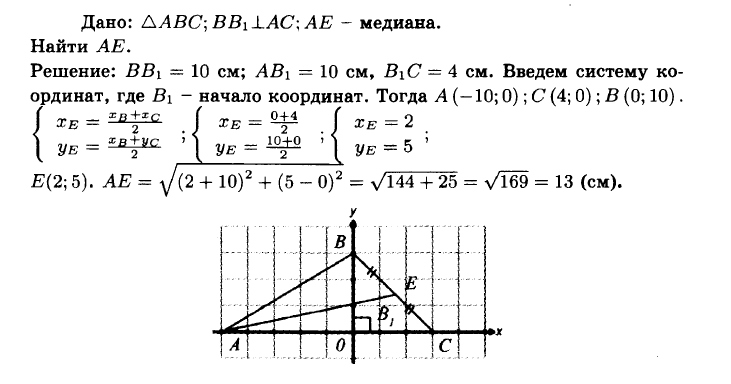
№942 Найдите медиану AM треугольника ABC, вершины которого имеют координаты: А (0; 1), В (1; —4), С (5; 2).
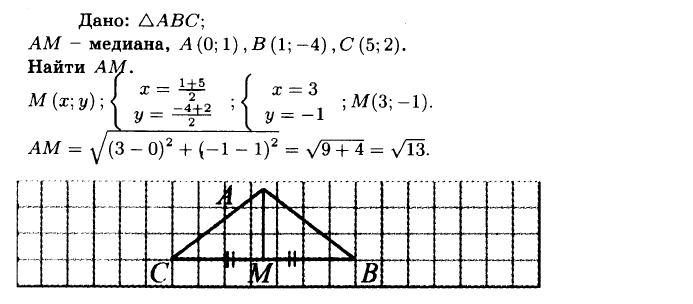
№943 Точки B и С лежат соответственно на положительных полуосях Ох и Оу, а точка А лежит на отрицательной полуоси Ох, причём ОА = а, ОВ = b, ОС = h. Найдите стороны АС и ВС треугольника ABC.
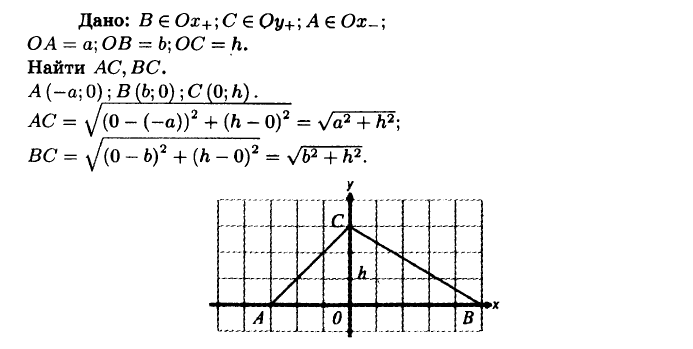
№944 Вершина А параллелограмма ОАСВ лежит на положительной полуоси Ох, вершина В имеет координаты (b; с), а ОА = а. Найдите:
а) координаты вершины С;
б) сторону АС и диагональ СО.
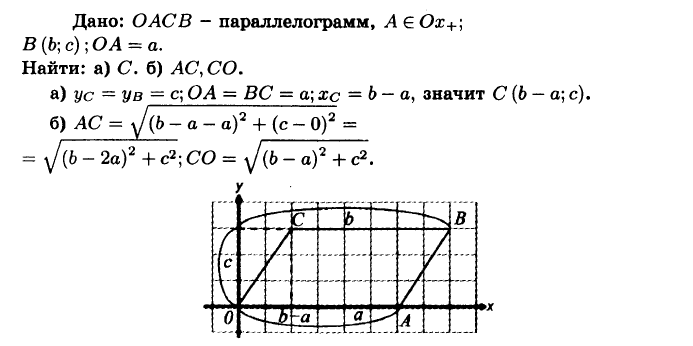
№945 Найдите сторону АС и диагональ ОС трапеции ОВСА с основаниями О А = а и ВС = d, если точка А лежит на положительной полуоси Ох, а вершина В имеет координаты (b; с).
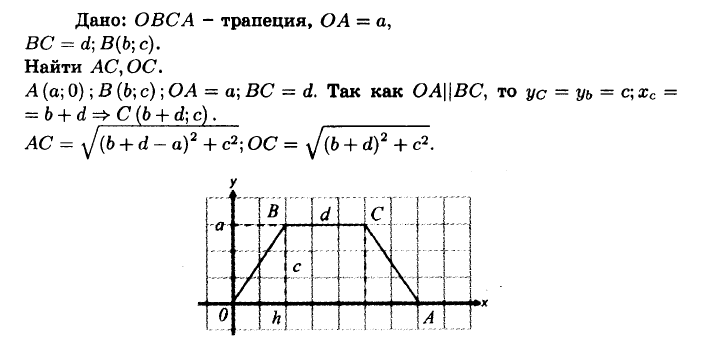
№946 Найдите х, если:
а) расстояние между точками А (2; 3) и В (х; 1) равно 2;
б) расстояние между точками М1 (—1; х) и М2 (2х; 3) равно 7.
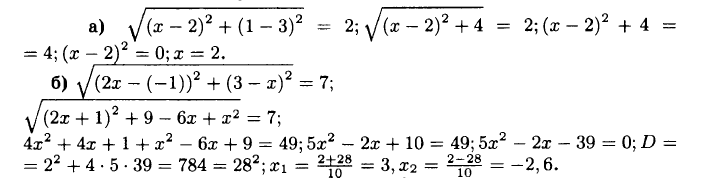
№947 Докажите, что треугольник ABC равнобедренный, и найдите его площадь, если вершины треугольника имеют координаты:
а) А (0; 1), В (1; —4), С (5; 2);
б) А (—4; 1), В (—2; 4), С (0; 1).
№948 На оси ординат найдите точку, равноудалённую от точек:
а) А (—3; 5) и B (6; 4);
б) С (4; —3) и D (8; 1).
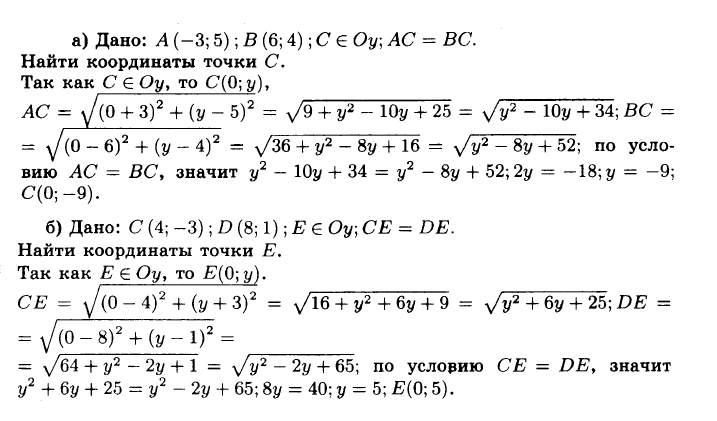
№949 На оси абсцисс найдите точку, равноудалённую от точек: а) А (1; 2) и B (—3; 4); б) С (1; 1) и D (3; 5).
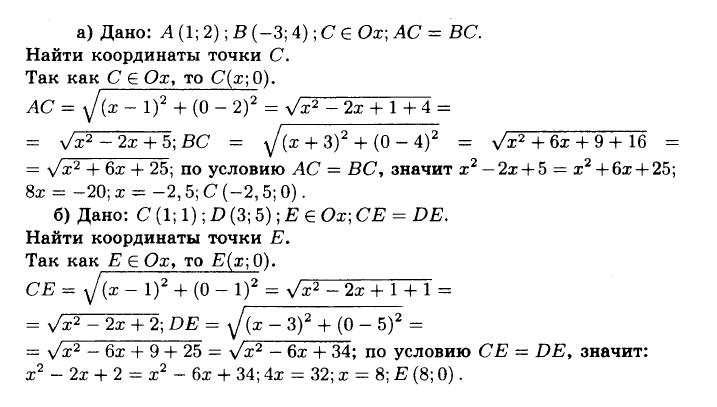
№950 Докажите, что четырёхугольник MNPQ является параллелограммом, и найдите его диагонали, если: а) М (1; 1), N(6; 1), Р(7; 4), Q (2; 4); б) М (—5; 1), N(-4; 4), Р(—1; 5), Q(—2; 2).
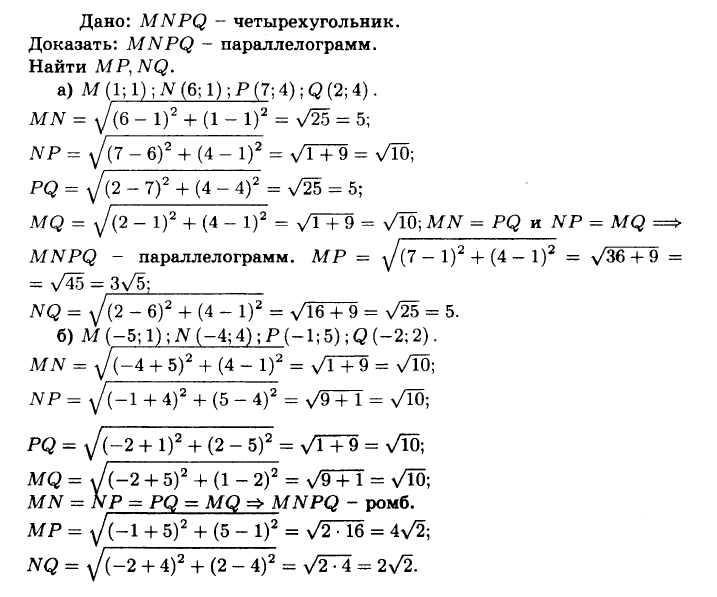
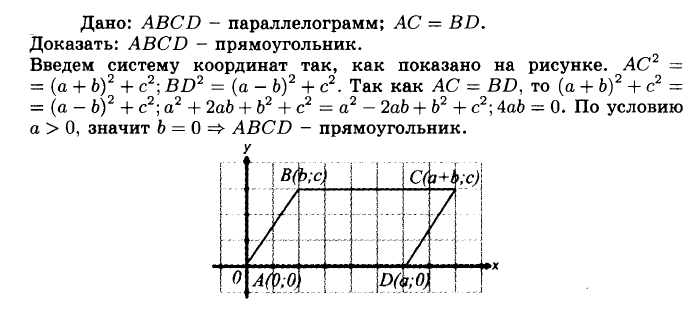
№951 Докажите, что четырёхугольник ABCD является прямоугольником, и найдите его площадь, если:
а) А (—3; —1), B (1; —1), С (1; —3), D (—3; —3);
б) А (4; 1), B (3; 5), С (—1; 4), D (0; 0).
№952 Докажите, что середина гипотенузы прямоугольного треугольника равноудалена от всех его вершин.
Решение в учебнике с. 233-234
ГДЗ. Ответы по геометрии. 9 класс. Учебник. Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Позняк Э.Г., Юдина И.И.
Глава Х Метод координат
§2 Простейшие задачи в координатах
№931 Начертите квадрат MNPQ так, чтобы вершина Р имела координаты (—3; 3), а диагонали квадрата пересекались в начале координат. Найдите координаты точек М, N и Q.
№932 Найдите координаты вершин равнобедренного треугольника ABC, изображённого на рисунке 281, если АВ = 2а, а высота СО равна h.
№933 Найдите координаты вершины D параллелограмма ABCD, если А (0; 0), В (5; 0), С (12; —3.).
№934 Найдите координаты вектора АВ, зная координаты его начала и конца: а) А (2; 7), В (—2; 7); б) А (—5; 1), В (—5; 27); в) А (—3; 0), В (0; 4); г) А (0; 3), В (—4; 0).
№935 Перечертите таблицу в тетрадь, заполните пустые клетки и найдите х и у:
№936 Перечертите таблицу в тетрадь и, используя формулы для вычисления координат середины М отрезка АВ, заполните пустые клетки:
№937 Даны точки А (0; 1) и В (5; —3). Найдите координаты точек С и D, если известно, что точка В — середина отрезка АС, а точка D — середина отрезка ВС.
№938 Найдите длины векторов:
а) а {5; 9};
б) b {-3; 4};
в) с {-10; -10};
г) d {10; 17};
д) е {11; -11};
е) f {10; 0}.
№939 Найдите расстояние от точки М (3; —2):
а) до оси абсцисс;
б) до оси ординат;
в) до начала координат.
№940 Найдите расстояние между точками А и В, если:
а) А (2; 7), В (—2; 7);
б) А (—5; 1), В (—5; —7);
в) А (—3; 0), В (0; 4);
г) А (0; 3), В(—4;0).
№941 Найдите периметр треугольника MNP, если М (4; 0), N (12; —2), Р (5; —9).
ГДЗ. Ответы по геометрии. 9 класс. Учебник. Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Позняк Э.Г., Юдина И.И.
Глава Х Метод координат
§2 Простейшие задачи в координатах
№929 Точка А лежит на положительной полуоси Ох, а точка В — на положительной полуоси Оу. Найдите координаты вершин треугольника АВО, если:
а) ОА = 5, ОВ = 3;
б) ОА = a, ОВ = b.
№930 Точка А лежит на положительной полуоси Ох, а точка В — на положительной полуоси Оу. Найдите координаты вершин прямоугольника ОАСВ, если:
а) ОА = 6,5, ОВ = 3;
б) ОА=а, ОВ = b.
