Monthly Archives: Июль 2022

8 класс. Алгебра. Никольский. Учебник. Ответы к стр. 22

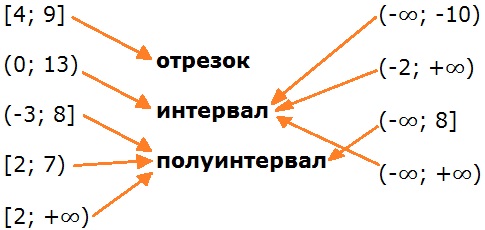
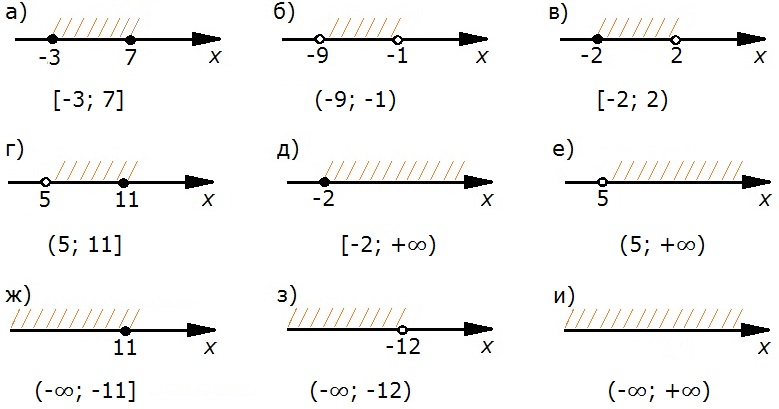
Простейшие функции. Квадратные корни
Функции и графики
Декартова система координат на плоскости

Ответы к стр. 22

48. Постройте данную точку и точки, симметричные ей относительно оси Oх, оси Oу, начала координат:
а) А(3; 5); б) В(-4; 2);
в) С(-4; -3); г) D(3; -5).
Определите координаты построенных точек.

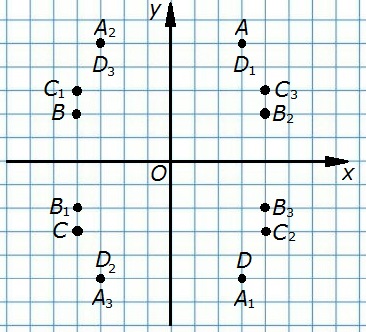
а) А(3; 5) - А₁(3; -5) симметрична относительно оси Ох, А₂(-3; 5) симметрична относительно оси Оу, А₃(-3; -5) симметрична относительно начала координат;

б) В(-4; 2) - В₁(-4; -2) симметрична относительно оси Ох, В₂(4; 2) симметрична относительно оси Оу, В₃(4; -2) симметрична относительно начала координат;

в) С(-4; -3) - С₁(-4; 3) симметрична относительно оси Ох, С₂(4; -3) симметрична относительно оси Оу, С₃(4; 3) симметрична относительно начала координат;

г) D(3; -5) - D₁(3; 5) симметрична относительно оси Ох, D₂(-3; -5) симметрична относительно оси Оу, D₃(-3; 5) симметрична относительно начала координат.

49. Симметричны ли относительно оси Oх, оси Oу, начала координат точки:
а) А(3; 2) и В(-3; 2);    б) С(2; 5) и D (2; -5);
в) М(-4; 3) и N(4; -3); г) E(-3; 1) и F(-3; -1);
д) Р(4; 5) и Q(-4; -5);  е) Х(-6; 7) и Y(6; 7)?

а) А(3; 2) и В(-3; 2) - симметричны относительно оси Оу;
б) С(2; 5) и D (2; -5) - симметричны относительно оси Ох;
в) М(-4; 3) и N(4; -3) - симметричны относительно начала координат;
г) E(-3; 1) и F(-3; -1) - симметричны относительно оси Ох;
д) Р(4; 5) и Q(-4; -5) - симметричны относительно начала координат;
е) Х(-6; 7) и Y(6; 7) - симметричны относительно оси Оу.

50. а) Постройте прямоугольник ABCD по координатам его вершин: А(0; 0), В(0; 8), С(5; 8), D (5; 0). Найдите периметр и площадь прямоугольника ABCD.
б) Постройте квадрат ABCD по координатам трёх его вершин: А(-2; -1), В(-2; 2), С(1; 2). Найдите координаты вершины D, периметр и площадь квадрата ABCD.

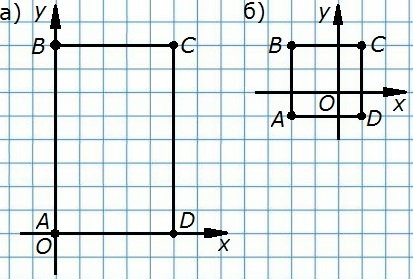
а) АВ = СD = 8, ВС = AD = 5,
Р = (8 + 5)•2 = 26,
S = 8•5 = 40;

б) D(1; -1), АВ = СD = ВС = AD = 3,
Р = 3•4 = 12,
S = 3•3 = 9.

51. Даны точки А(3; 5) и В(10; -9). Определите координаты точки С, если:
а) С - середина отрезка АВ; б) А - середина отрезка ВС;
в) АС : СВ = 2 : 5;                       г) АС : СВ = 4 : 3.

а) С_х = ^А_х+В_х/₂ = ³⁺¹⁰/₂ = 6,5,
С_у = ^А_у+В_у/₂ = ^5+(-9)/₂ = -2,
С(6,5; -2);

б) А = ^В+С/₂ ⇒ С = 2А - В,
С_х = 2А_х - В_х = 2•3 - 10 = -4,
С_у = 2А_у - В_у = 2•5 - (-9) = 19,
С(-4; 19);

в) из задания 28 (стр. 14): х = (nх₁ + mх₂)/(m + n),
С_х = ^{5А_х+2В_х}/₂₊₅ = ^5•3+2•10/₇ = 5,
С_у = ^{5А_у+2В_у}/₂₊₅ = ^{5•5+2•(-9)}/₇ = 1,
С(5; 1);

г) из задания 28 (стр. 14): х = (nх₁ + mх₂)/(m + n),
С_х = ^{3А_х+4В_х}/₄₊₃ = ^3•3+4•10/₇ = 7,
С_у = ^{3А_у+4В_у}/₄₊₃ = ^{3•5+4•(-9)}/₇ = -3,
С(7; -3).

52. Ищем информацию. Используя учебник, справочную литературу и Интернет, подготовьте сообщение о Р. Декарте, его жизни и вкладе в науку.

Рене Декарт - французский философ, математик и естествоиспытатель, один из основоположников философии Нового времени, создавший аналитическую геометрию и современную алгебраическую символику, одна из ключевых фигур научной революции. Декарт происходил из старинного, но обедневшего дворянского рода, был младшим (третьим) сыном в семье. Родился 31 марта 1596 года в городе Ла-Э-ан-Турен (сейчас Декарт), департамент Эндр и Луара, Франция. Его мать Жанна Брошар умерла, когда ему был 1 год. Отец, Жоаким Декарт, был судьёй и советником парламента в городе Ренн и в Лаэ появлялся редко, воспитанием мальчика занималась бабушка по матери. В детстве Рене отличался хрупким здоровьем и невероятной любознательностью, его стремление к науке было настолько сильно, что отец в шутку стал называть Рене своим маленьким философом.
Главный философско-математический труд Декарта – книга «Рассуждение о методе», состоящая из нескольких приложений. В одном приложении он излагал аналитическую геометрию, во втором знакомил с правилами работы оптических явлений и приборов. Главным достижением Рене стало изложение закона о преломлении света, который до него никто не мог составить. Он придумал обозначение неизвестных символов буквами «x, y, z», а постоянных величин буквами «α, b, c». Декарт трудился над разработкой канонической формы уравнений, используемой по настоящий день - это когда правая сторона уравнения равна нулю. Именно Рене придумал современную систему координат, сыгравшую важную роль в совершенствовании двух точных наук - физики и математики. Он использовал её для того, чтобы стало возможным описать геометрические свойства кривых и тел, используя классическую алгебру. Благодаря этому нововведению появилась возможность более подробной и точной трактовки отрицательных чисел.

Ответы по алгебре. 8 класс. Учебник. Никольский С. М., Потапов М. К., Решетников Н. Н., Шевкин А. В.

Алгебра. 8 класс

8 класс. Алгебра. Никольский. Учебник. Ответы к стр. 21

Простейшие функции. Квадратные корни
Функции и графики
Декартова система координат на плоскости

Ответы к стр. 21

43. Для каких точек координатной плоскости:
а) абсцисса равна нулю;       б) ордината равна нулю;
в) абсцисса положительна; г) ордината положительна?

а) для точек, лежащих на оси Оу;
б) для точек, лежащих на оси Ох;
в) для точек, лежащих в I и VI координатных четвертях;
г) для точек, лежащих в I и II координатных четвертях.

44. Какими свойствами обладают:
а) координаты точек I, II, III, IV четвертей;
б) координаты точек, симметричных относительно оси Ох, оси Оу, начала координат?

а) у координат точек I четверти абсцисса положительна, ордината положительна (x > 0, у > 0);
у координат точек II четверти абсцисса отрицательна, ордината положительна (x < 0, у > 0);
у координат точек III четверти абсцисса отрицательна, ордината отрицательна (x < 0, у < 0);
у координат точек IV четверти абсцисса положительна, ордината отрицательна (x > 0, у < 0);

б) у точек, симметричных относительно оси Ох, абсциссы одинаковы, а ординаты противоположны по знаку: х₁ = х₂, у₁ = -у₂;
у точек, симметричных относительно оси Оу, абсциссы противоположны по знаку, а ординаты одинаковы: х₁ = -х₂, у₁ = у₂;
у точек, симметричных относительно начала координат, абсциссы противоположны по знаку и ординаты противоположны по знаку: х₁ = -х₂, у₁ = -у₂.

45. Назовите абсциссу и ординату точки:
а) А(-2; 3); б) В(3; -2); в) С(6; 5); г) D(-2; -6).
Какой координатной четверти принадлежит эта точка?

а) А(-2; 3): -2 - абсцисса, 3 - ордината, II координатная четверть;
б) В(3; -2): 3 - абсцисса, -2 - ордината, IV координатная четверть;
в) С(6; 5): 6 - абсцисса, 5 - ордината, I координатная четверть;
г) В(-2; -6): -2 - абсцисса, -6 - ордината, III координатная четверть.

46. Определите по координатам точки, в какой четверти координатной плоскости она расположена:
а) (12; 5); б) (-3; -4); в) (7; -3); г) (-8; 13).

а) (12; 5) - I четверть;
б) (-3; -4) - III четверть;
в) (7; -3) - IV четверть;
г) (-8; 13) - II четверть.

47. Постройте точку, симметричную точке:
а) А(1; 3) относительно оси Оу;
б) В(-2; -1) относительно оси Ох;
в) С(3; -2) относительно точки О(0; 0).

а) А(1; 3) - А₁(-1; 3) симметрична относительно оси Оу;
б) В(-2; -1) - В₁(-2; 1) симметрична относительно оси Ох;
в) С(3; -2) - С₁(-3; 2) симметрична относительно точки О(0; 0).

Ответы по алгебре. 8 класс. Учебник. Никольский С. М., Потапов М. К., Решетников Н. Н., Шевкин А. В.

Алгебра. 8 класс

8 класс. Алгебра. Потапов, Шевкин. Рабочая тетрадь №1. Ответы к стр. 12

Функции и графики
Множества чисел

25^∗. На рисунке схематически изображены числовые множества N₀ (множество неотрицательных целых чисел), Z, Q, R - каждое следующее множество включает в себя предыдущее. Покажите стрелкой, в какую часть этих множеств входят указанные числа.

26^∗. Изобразите на координатной оси все числа х, удовлетворяющие равенству или неравенству, записанному над ней:

Ответы по алгебре. Рабочая тетрадь. 8 класс. Часть 1. Потапов М.К., Шевкин А.В.

Алгебра. 8 класс

8 класс. Алгебра. Потапов, Шевкин. Рабочая тетрадь №1. Ответы к стр. 11

Функции и графики
Множества чисел

21. По рисунку из задания 20 установите соответствие между изображением числового множества и его названием:
отрезок: а)     интервал: б), …     полуинтервал: в), …

Отрезок: а).
Интервал: б), ж), з), и).
Полуинтервал: в), г), д), е).

22. Установите соответствие между обозначением числового множества и его названием при помощи стрелки:

23. Изобразите на координатной оси числовой промежуток, указанный под ней:

24. Запишите с помощью знаков ∈, ∉ и обозначений множеств чисел N, Z, Q, R верное высказывание:

а) число 0 не является натуральным числом: 0 ∉ N;
б) число 0 является целым числом: 0 ∈ Z;
в) число 5 является натуральным числом: 5 ∈ N;
г) число -5 не является натуральным числом: -5 ∉ N;
д) число ²/₃ является рациональным числом: ²/₃ ∈ Q;
е) число ²/₃ не является целым числом: ²/₃ ∉ Z;
ж) число -0,(6) является рациональным числом: -0,(6) ∈ Q;
з) число -0,(6) не является иррациональным числом: -0,(6) ∉ I;
и) число 0,1011011101… не является рациональным числом: 0,1011011101… ∉ Q;
к) число 0,1011011101… является действительным числом: 0,1011011101… ∈ R.

Замечание. Предполагается, что правило записи цифр в дробной части числа сохраняется: в заданиях и) и к) после каждого нуля пишут на одну единицу больше, чем было записано до этого нуля.

Ответы по алгебре. Рабочая тетрадь. 8 класс. Часть 1. Потапов М.К., Шевкин А.В.

Алгебра. 8 класс

8 класс. Алгебра. Потапов, Шевкин. Рабочая тетрадь №1. Ответы к стр. 10

Функции и графики
Множества чисел

19. Запишите во второй строке таблицы числовой промежуток, соответствующий неравенству, данному в первой строке таблицы:

20. Запишите обозначение числового промежутка, изображённого на рисунке:

а) [2; 5];
б) (2; 5);
в) [2; 5);
г) (2; 5];
д) [2; +∞);
е) (-∞; 5];
ж) (2; +∞);
з) (-∞; 5);
и) (-∞; +∞).

Ответы по алгебре. Рабочая тетрадь. 8 класс. Часть 1. Потапов М.К., Шевкин А.В.

Алгебра. 8 класс