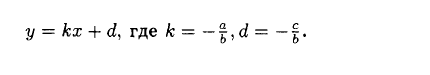Monthly Archives: Ноябрь 2023

9 класс. Геометрия. Атанасян Л.С. Учебник. Ответы к стр. 251

ГДЗ. Ответы по геометрии. 9 класс. Учебник. Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Позняк Э.Г., Юдина И.И.

 

Глава ХI Соотношения между сторонами и углами треугольника. .скалярное произведение векторов

§1 Синус, косинус, тангенс, котангенс угла

№1011 Ответьте на вопросы:

а) Может ли абсцисса точки единичной полуокружности иметь значения 0,3; 1/3; –1/3; 5/3; –2,8?

б) Может ли ордината точки единичной полуокружности иметь значения 0,6; 1/7; –0,3; 7; 1,002? Ответы обоснуйте.

---

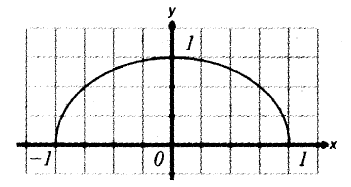
№1012 Проверьте, что точки M₁ (0; 1), М₂ (1/2; √3/2), M₃ (√2/2; √2/2), M₄ (√2/2; 1/2), В (–1; 0) лежат на единичной полуокружности. Выпишите значения синуса, косинуса и тангенса углов AOM₁, АОМ₂, АОМ₃, АОМ₄, АОВ.

---

№1013 Найдите sin а, если:

a) cos a = 1/2;
б) cos a = –2/3;
в) cos a = –1.

---

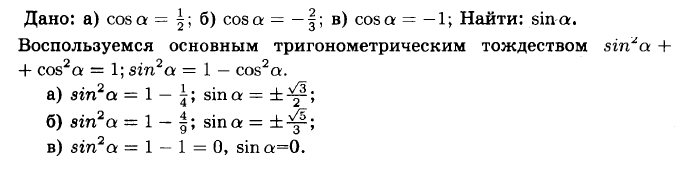
№1014 Найдите cos а, если:

a) sin a = √3/2;
б) sin a = 1/4;
в) sin a = 0.

---

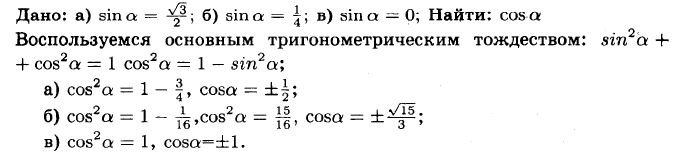
№1015 Найдите tg а, если:

а) cos a = 1;
б) cos a = –√3/2;
в) sin a = √2/2 и 0° < а < 90°;
г) sin a = 3/5 и 90° < а < 180°.

---

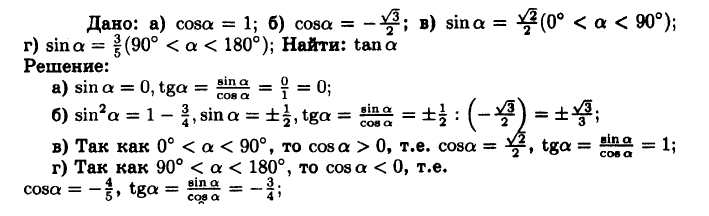
№1016 Вычислите синусы, косинусы и тангенсы углов 120°, 135°, 150°.

---

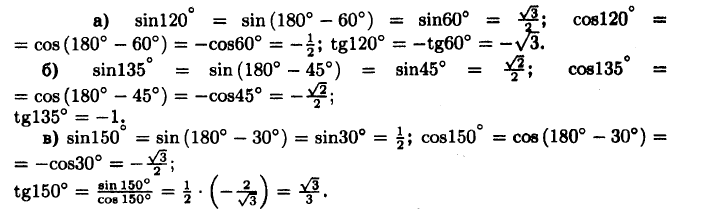
№1017 Постройте ∠А, если:

а) sin А = 2/3;
б) cos А = 3/4;
в) cos А = –2/5 

---

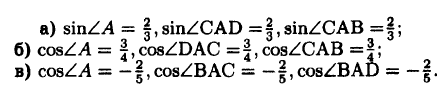
№1018 Угол между лучом ОА, пересекающим единичную полуокружность, и положительной полуосью Ох равен α. Найдите координаты точки А, если:
а) ОА = 3, α = 45°;
б) ОА = 1,5, α = 90°;
в) ОА = 5, α = 150°;
г) ОА = 1, α= 180°;
д) ОА = 2, α = 30°.

---

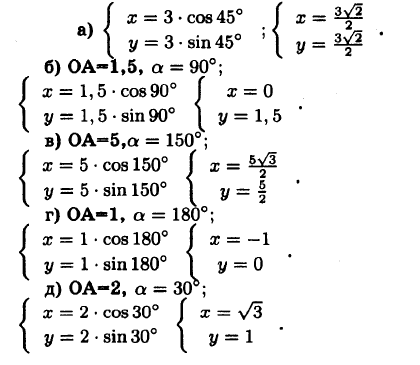
№1019 Найдите угол между лучом ОА и положительной полуосью Ох, если точка А имеет координаты:

а) (2; 2);
б) (0; 3);
в) (–√3; 1);
г) (–2√2; 2√2).

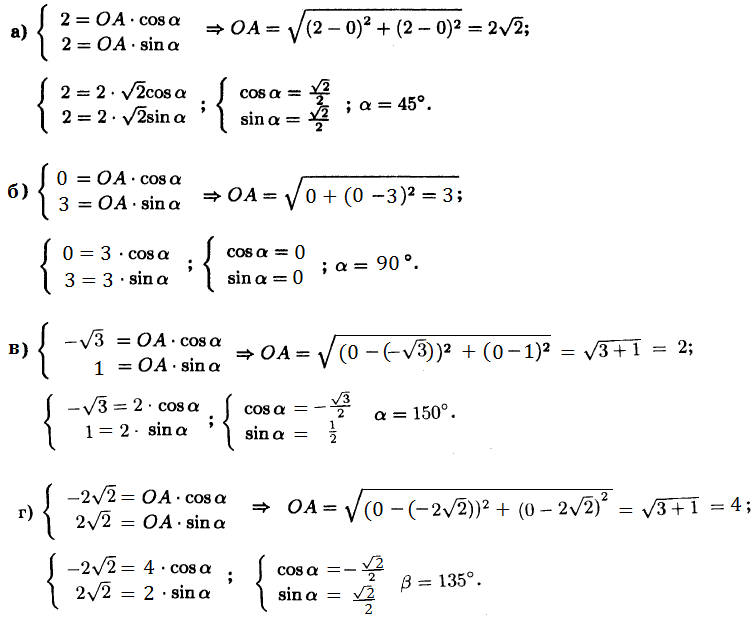
   ← Предыдущая         Следующая →

Геометрия. 9 класс. ГДЗ

9 класс. Геометрия. Атанасян Л.С. Учебник. Ответы к стр. 247

ГДЗ. Ответы по геометрии. 9 класс. Учебник. Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Позняк Э.Г., Юдина И.И.

 

Глава Х Метод координат

Дополнительные задачи к главе X. Метод координат

№1005 Докажите, что точки А, В и С лежат на одной прямой, если:

а) А (—2; 0), В (3; 3/2), С (6; 4);

б) А (3; 10), В (3; 12), С (3; —6);

в) А (1; 2), В (2; 5), С (—10; —31). 

 

---

Применение метода координат к решению задач

№1006 Две стороны треугольника равны 17 см и 28 см, а высота, проведённая к большей из них, равна 15 см. Найдите медианы треугольника.

---

№1007 Докажите, что отрезок, соединяющий середины диагоналей трапеции, равен полуразности оснований.

---

№1008 Дан параллелограмм ABCD. Докажите, что для всех точек М величина (AM² + СМ²) - (ВМ² + DM²) имеет одно и то же значение.

---

№1009 Докажите, что медиану АА1 треугольника ABC можно вычислить по формуле АА1 =1/2 корень(2АС2 + 2АВ2 — ВС2). Используя эту формулу, докажите, что если две медианы треугольника равны, то треугольник равнобедренный.

---

№1010 Даны две точки А та В. Найдите множество всех точек М, для каждой из которых:
а) 2AM² — ВМ² = 2АВ²;

б) 2 AM² + 2ВМ² = 6 АВ².

   ← Предыдущая         Следующая →

Геометрия. 9 класс. ГДЗ

9 класс. Геометрия. Атанасян Л.С. Учебник. Ответы к стр. 246 Дополнительные задачи к главе X. Метод координат

ГДЗ. Ответы по геометрии. 9 класс. Учебник. Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Позняк Э.Г., Юдина И.И.

 

Глава Х Метод координат

Дополнительные задачи к главе X. Метод координат

№992 Докажите, что треугольник АВС, вершины которого имеют координаты А (4; 8), В (12; 11), С (7; 0), является равнобедренным, но не равносторонним.

 

---

№993 Докажите, что углы А и С треугольника АВС равны, если А (—5; 6), В (3; —9) и С (—12; —17).

---

№994 Докажите, что точка D равноудалена от точек А, В и С, если:

а) D (1; 1), А (5; 4), В (4; —3), С (—2; 5);

б) D (1; 0), А (7; —8), В (—5; 8), С (9; 6).

---

№995 На оси абсцисс найдите точку, равноудалённую от точек М, (-2; 4) и М2 (6; 8).

---

№996 Вершины треугольника АВС имеют координаты А (—5; 13), В (3; 5), С (—3; —1). Найдите:

а) координаты середин сторон треугольника; 

б) медиану, проведённую к стороне АС;

в) средние линии треугольника.

---

№997 Докажите, что четырёхугольник ABCD, вершины которого имеют координаты А (3; 2), В (0; 5), С (—3; 2), D (0; —1), является квадратом.

---

№998 Докажите, что четырёхугольник ABCD, вершины которого имеют координаты А (—2;—3), 13 (1; 4), С (8; 7), D (5; 0), является ромбом. Найдите его площадь.

---

№999 Найдите координаты четвёртой вершины параллелограмма по заданным координатам трёх его вершин: (—4; 4), (—5; 1) и (—1; 5). Сколько решений имеет задача?

---

№1000 Выясните, какие из данных уравнений являются уравнениями окружности. Найдите координаты центра и радиус каждой окружности:
а) (х — 1)² + (y + 2)² = 25;
б) х² + (у + 7)² = 1;
в) х² + у² + 8х — 4у + 40 = 0;
г) х² + у² — 2х + 4у - 20 = 0;
д) х² + у² — 4х — 2у + 1 =0.

---

№1001 Напишите уравнение окружности, проходящей через точки А (3; 0) и В (—1; 2), если центр её лежит на прямой у = х + 2.

---

№1002 Напишите уравнение окружности, проходящей через три данные точки:

а) А (1; —4), В (4; 5), С (3; —2);

б) А (3; —7), В (8; —2), С (6; 2).

---

№1003 Вершины треугольника АВС имеют координаты А (—7; 5), В (3; —1), С (5; 3). Составьте уравнения:

а) серединных перпендикуляров к сторонам треугольника;

 

б) прямых АВ, ВС и СА;

в) прямых, на которых лежат средние линии треугольника.

---

№1004 Докажите, что прямые, заданные уравнениями 3х — 1,5y + 1 = 0 и 2х — у — 3 = 0, параллельны.

   ← Предыдущая         Следующая →

Геометрия. 9 класс. ГДЗ

9 класс. Геометрия. Атанасян Л.С. Учебник. Ответы к стр. 245 Дополнительные задачи к главе X. Метод координат

ГДЗ. Ответы по геометрии. 9 класс. Учебник. Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Позняк Э.Г., Юдина И.И.

 

Глава Х Метод координат

Дополнительные задачи к главе X. Метод координат

№988 Векторы а и b не коллинеарны. Найдите такое число х (если это возможно), чтобы векторы р и q были коллинеарны:

а) p = 2a — b, q = a + xb;

б) р = xa — b, q — a + xb;

в) р = а + xb, q = а — 2b;

г) p = 2a + b, q = xa + b

---

№989 Найдите координаты вектора р и его длину, если:

а) р = 7а — 3b, а {1; —1}, b {5; —2};

б) р = 4а — 2b, а {6; 3}, b {5; 4};

в) р = 5а — 4b, а {3/5;1/5}, b {6; —1};

г) р = 3 (—2а — 4b), а {1; 5}, b {—1; —1}.

---

№990 Даны векторы а {3; 4}, b {6; —8}, с {1;5}.

а) Найдите координаты векторов p = a + b,q = b + c, r=2a — b + с, s = а — b — с.

б) Найдите |а|, | b |, |р|, |q|.

---

№991 Докажите, что расстояние между любыми двумя точками М₁ (x₁; 0) и М₂ (х₂; 0) оси абсцисс вычисляется по формуле d = |х₁ — х₂|.

   ← Предыдущая         Следующая →

Геометрия. 9 класс. ГДЗ

9 класс. Геометрия. Атанасян Л.С. Учебник. Ответы к стр. 244-245 Вопросы для повторения к главе X. Метод координат

ГДЗ. Ответы по геометрии. 9 класс. Учебник. Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Позняк Э.Г., Юдина И.И.

 

Глава Х Метод координат

Вопросы для повторения к главе X. Метод координат

1 Сформулируйте и докажите лемму о коллинеарных векторах.

2 Что значит разложить вектор по двум данным векторам?

3 Сформулируйте и докажите теорему о разложении вектора по двум неколлинеарным векторам.

4 Объясните, как вводится прямоугольная система координат.

5 Что такое координатные векторы?

6 Сформулируйте и докажите утверждение о разложении произвольного вектора по координатным векторам.

7 Что такое координаты вектора? Чему равны координаты координатных векторов? Как связаны между собой координаты равных векторов?

8 Сформулируйте и докажите правила нахождения координат суммы и разности векторов, а также произведения вектора на число по заданным координатам векторов.

9 Что такое радиус-вектор точки? Докажите, что координаты точки равны соответствующим координатам её радиус-вектора.

10 Выведите формулы для вычисления координат вектора по координатам его начала и конца.

11 Выведите формулы для вычисления координат середины отрезка по координатам его концов.

12 Выведите формулу для вычисления длины вектора по его координатам.

13 Выведите формулу для вычисления расстояния между двумя точками по их координатам.

14 Приведите пример решения геометрической задачи с применением метода координат.

15 Какое уравнение называется уравнением данной линии? Приведите пример.

16 Выведите уравнение окружности данного радиуса с центром в данной точке.

17 Напишите уравнение окружности данного радиуса с центром в начале координат.

x² + y² = r².

 

18 Выведите уравнение данной прямой в прямоугольной системе координат.

19 Что такое угловой коэффициент прямой?

20 Докажите, что: две параллельные прямые, не параллельные оси Оу, имеют одинаковые угловые коэффициенты; если две прямые имеют одинаковые угловые коэффициенты, то эти прямые параллельны.

21 Напишите уравнения прямых, проходящих через данную точку М₀ (x₀; y₀) и параллельных осям координат.

y = x₀; x = y_0.

22 Напишите уравнения осей координат.

y = 0 — ось Ox; x = 0 — ось Оу.

23 Исследуйте взаимное расположение двух окружностей в зависимости от их радиусов и расстояния между их центрами. Сформулируйте полученные выводы.

24 Приведите примеры использования уравнений окружности и прямой при решении геометрических задач.

   ← Предыдущая         Следующая →

Геометрия. 9 класс. ГДЗ